Sic Bo Dice

Sic Bo is a casino bidding game. There is a dealer who takes bets and rolls the dice and players who can make bids on the mat. There can be any number of players making bids at a time as long as each player has their own colored chip to distinguish them. Sic Bo is a gambling game and is usually played for money. Originating from China, Sic Bo is a dice game that is quickly growing in popularity. In Chinese, Sic Bo is called Tai Sai or Dai Siu, which literally means 'Big Small' in English. If you have never been to Macau to see Sic Bo in action, then you have been missing out on a real cultural experience. Sic Bo is an ancient Chinese dice game that sees players gambling on the three dice roll results. Its direct translation is valuable dice, and also, confusingly, dice pair. In the early 1900s, this popular Chinese game of luck came into the western world.

The Mathematics of Sic Bo

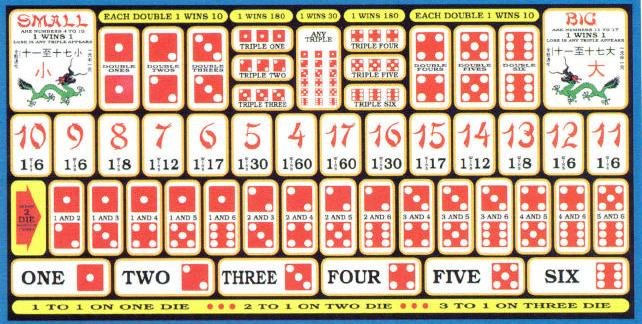
Sic Bo – The name of this Chinese dice game, which literally translates as 'dice pair.' Shaker – A device that looks a bit like a snow globe, used to mix up the dice. Small – A wager that total of the three dice will be between 4 and 10.

By

Michael Shackleford

January 21, 2005

Sic Bo, meaning 'dice pair' is an ancient Chinese gambling game. Today it is one of the lesser known casino games and is often confined to designated rooms for Asian games. The game uses three dice and a table with a variety of betting options on the roll of those dice. The odds and table layout may also vary from place to place. If you must play Sic Bo I would suggest sticking to only the 'low' and 'high' bets.

Following is a list of the bets available. The payoffs listed are for Atlantic City and the Mirage in Las Vegas. Other casino's odds will vary.

Sic Bo The 3 Dice Game - Strategy, How To Play , Rules And Odds

• Small: Wins on total of 4-10, except for a three of a kind. Pays 1 to 1.
• Big: Wins on total of 11-17, except for a three of a kind. Pays 1 to 1.
• 4: Wins on total of 4. Pays 60 to 1.
• 5: Wins on total of 5. Pays 30 to 1.
• 6: Wins on total of 6. Pays 17 to 1.
• 7: Wins on total of 7. Pays 12 to 1.
• 8: Wins on total of 8. Pays 8 to 1.
• 9: Wins on total of 9. Pays 6 to 1.
• 10: Wins on total of 10. Pays 6 to 1.
• 11: Wins on total of 11. Pays 6 to 1.
• 12: Wins on total of 12. Pays 6 to 1.
• 13: Wins on total of 13. Pays 8 to 1.
• 14: Wins on total of 14. Pays 12 to 1.
• 15: Wins on total of 15. Pays 17 to 1.
• 16: Wins on total of 16. Pays 30 to 1.
• 17: Wins on total of 17. Pays 60 to 1.

• Two of a kind: Player may bet on any of the 15 possible two dice combinations (for example a 1 and 2). Bet wins if both numbers appear. Probability of winning is 13.89%. Pays 5 to 1.
• Double: Player may bet on any specific number (for example a 1). Player wins if at least 2 of the 3 dice land on that number. Probability of winning is 7.41%. Pays 10 to 1.
• Triple: Player may bet on any specific number (for example a 1). Player wins if all 3 dice land on that number. Probability of winning is 0.46%. Pays 180 to 1.
• Any Triple: Wins on any three of a kind. Pays 30 to 1.
• Individual Number: Player may bet on any specific number from 1 to 6. If chosen number appears 1 time bet pays 1 to 1, if it appears 2 times bet pays 2 to 1, and if it appears 3 times it pays 3 to 1.

The critical step in calculating the odds in Sic Bo is to find the probability of any given total in the throw of three dice. Following is a formula for s spots over n dice, taken from The Theory of Gambling and Statistical Logic by Richard A. Epstein, formula 5-14.

For example, let's look at the number of ways to get 11 spots over 3 dice.

int[(s-n)/6] = int[(11-3)/6] = int[1.33] = 1

The total would be 6^-3 * [-1⁰*combin(3,0)*combin(11-6*0-1,3-1) + -1¹*combin(3,1)*combin(11-6*1-1,3-1) ] =
1/218 * [1*1*combin(10,2) + -1*3*combin(4,2)] =
1/218 * [1*1*45 + -1*3*6] =
1/218 * [45-18] = 27/216 = 12.50%

Alternatively, if you can program a computer that would probably be the fastest way to get the results.

Here is a simple function in C++.

Following is the output of the function.

If you don't know how to program you're going to have to do this the hard way. What I recommend is list every combination of 3 dice. To avoid the list being 6³=216 items long do not repeat the same combinations in different orders. In the interests of not listing the same number twice always order each combination from lowest to highest, not forgetting combinations with a pair or three of a kind.

So we start with 1,1,1.

Next would be 1,1,2.

Then 1,1,3; 1,1,4; 1,1,5; and 1,1,6.

Obviously you can't roll a 7 with one dice so next we increment the second die.

1,2,?

The third die must be greater or equal to the second die so the next combination in full would be 1,2,2.

Next comes 1,2,3; 1,2,4; 1,2,5; and 1,2,6.

Then comes 1,3,3.

I hope you see the pattern. The whole list would look like the following.

Next we have to determine the number of permutations of each combination. A combination is a set without regard to order and a permutation is a set with regard to order.

With a three of a kind there is only one way permutation. For example if the three dice are 1,1,1 there is only one way to roll that a 1 each time.

If the combination is 1,1,2 there are three ways to roll that: 1,1,2; 1,2,1; and 2,1,1.

If all three dice are 1,2,3 there are six possible permutations: 1,2,3; 1,3,2; 2,1,3; 2,3,1; 3,1,2; 3,2,1

The general formula is that if you have a total of d dice and the totals of each number are x₁, x₂, x₃…x_n then the number of permutations are d!/(x₁!*x₂!*x₃*…*x_n). So the number of ways to get a three of a kind would be 3!/3! = 6/6 = 1. The number of ways to get a pair would be 3!/(2!*1!) = 6/(2*1) = 3. The number of ways to get three different numbers would be 3!/(1!*1!*1!) = 6/(1*1*1) = 6.

Next we go through the tedious process of adding the number of permutations for each total. For example a total of 6 has the following combinations with the corresponding number of permutations.

The final table will look like this, not unlike the result of the computer function earlier.

So now lets add a column to our list for the number of combinations of each set. Let's also add a total for the three dice.

Now we can divide each total number permutations by the total number 3-dice permutations (216) to get the probability of each total.

Finally, we are ready to evaluate the expected value of each bet. The expected value is the ratio of the amount the player can expect to win to the amount he bets on any given bet. So a fair bet would an expected value of zero. A positive expected value would mean the player has the advantage. A negative expected value would mean the dealer has the advantage.

Let's start with the 4 bet. This wins with a total of 4 and pays 60 to 1. For those who don't know, '60 to 1' means if the player wins he wins 60 times his bet and KEEPS his original wager. Had the odds paid '60 for 1' the player would NOT keep his original bet. Most table games pay on a 'to 1' basis.

The probability of a total of 4 is 3/216 = 0.013889. Thus the probability of losing is 1-(3/216) = 1-0.013889 = 0.986111.

The expected value of any bet with only two possibilities, winning or losing, is:

(Probability of winning)*(Amount of win) + (Probability of losing)*(Amount of loss).

For the 4 bet the expected value is

0.013889 * 60 - 0.986111*-1 = -0.15278.

So, this tells us that for every dollar the player bets on a total of 4 he can expect to lose 15.278 cents on average. Or, the house edge is 15.278%.

The next table shows the expected value and how it was calculated for all bets of a total of 4 to 17.

Two of a kind

There are combin(6,2)=6!/(4!*2!)=15 ways to choose two numbers out of six. Each of these combinations is listed on the table and the player bet on as many as he wishes. If both numbers appear on the roll of the three dice then the player wins and is paid 15 to 1.

Let's assume the player picks a 1 and 2 as his two numbers. What is the probability that both a 1 and 2 occur in the roll of 3 dice? One way to do this would be to note all the possible winning permutations:

Thus there are a total of 30 winning permutations.

There are 6³=216 total permutations, so the probability of winning is 30/216 = 1/36 = 0.1388889

The two of a kind bet pays 5 to 1. So the expected value is 0.1388889*5 + (1-0.1388889)*-1 = -0.16667. In other words the house edge is 16.67%.

Double

There are six double bets available, one for each number from 1 to 6. The player may be on any one or combination of bets. Any given bet wins if at least two of the three dice land on that number.

Let's assume the player bets on the 1.

One way to solve it would be to note all the winning permutations:

Thus there are a total of 16 winning permutations.

There are 6³=216 total permutations, so the probability of winning is 16/216 = 0.0740741.

The double bet pays 10 to 1. So the expected value is 0.0740741*10 + (1-0.0740741)*-1 = -0.18518. In other words the house edge is 18.52% (ouch!).

Triple

Player may bet on any specific number (for example a 1). Player wins if all 3 dice land on that number.

There is obviously only one way to win this bet, so the probability of winning is 1/216 = 0.0046296. The bet pays 180 to 1 so the expected value is 0.0046296*180 + (1-0.0046296)*-1 = -0.16204. So the house edge is 16.204%.

Any Triple

The Any Triple bet pays if any three of a kind is thrown. There are obviously six winning combinations (1,1,1; 2,2,2; 3,3,3; etc.). So the probability of winning is 6/216 = 0.027778. The bet pays 30 to 1 so the expected value is 0.027778*30 + (1-0.027778)*-1 = -0.13889. So the house edge is 13.89%.

Low

The low bet wins if the total of the three dice is 3 to 10, without being a three of a kind. The probability of any total 10 or less is exactly 50%. The average number on any one die is (1+2+3+4+5+6)/6 = 21/6 = 3.5. So the average of three dice is 3*3.5 = 10.5. It stands to reason that the probability of getting under or over 10.5 is 50%.

See Full List On Gambledex.com

However the bet loses on a three of a kind. There are 3 three of a kinds that would turn a winner into a loser: 1,1,1; 2,2,2; and 3,3,3. So the probability of having a total of 10 or less as a three of a kind is 3/216 = 0.0188889. So the overall probability of winning is 0.5 – 0.188889 = 0.4861111. The bet pays 1 to 1 so the expected value is 0.4861111*1 + (1-0.4861111)*-1 = -0.02778. Thus the house edge is 2.78%.

High

The high is just the opposite of the low bet, so it stands to reason the house edge would also be 2.78%.

Individual Number

Player may bet on any specific number from 1 to 6. If chosen number appears 1 time bet pays 1 to 1, if it appears 2 times bet pays 2 to 1, and if it appears 3 times it pays 3 to 1. Probability of 1 match is 34.72%, 2 matches is 6.94%, 3 matches is 0.46%.

Let's assume the player picks the number one.

There is only one way to get three ones: 1,1,1. So the probability of three ones is 1/6³ = 1/216.

Following are the ways to get two 1's and the number of permutations of each.

So the probability of two ones is 15/6³ = 15/216.

Following are the ways to get one 1 and the number of permutations of each.

So the probability of two ones is 75/6³ = 75/216.

Then 1,1,3; 1,1,4; 1,1,5; and 1,1,6.

Obviously you can't roll a 7 with one dice so next we increment the second die.

1,2,?

The third die must be greater or equal to the second die so the next combination in full would be 1,2,2.

Next comes 1,2,3; 1,2,4; 1,2,5; and 1,2,6.

Then comes 1,3,3.

I hope you see the pattern. The whole list would look like the following.

Next we have to determine the number of permutations of each combination. A combination is a set without regard to order and a permutation is a set with regard to order.

With a three of a kind there is only one way permutation. For example if the three dice are 1,1,1 there is only one way to roll that a 1 each time.

If the combination is 1,1,2 there are three ways to roll that: 1,1,2; 1,2,1; and 2,1,1.

If all three dice are 1,2,3 there are six possible permutations: 1,2,3; 1,3,2; 2,1,3; 2,3,1; 3,1,2; 3,2,1

The general formula is that if you have a total of d dice and the totals of each number are x₁, x₂, x₃…x_n then the number of permutations are d!/(x₁!*x₂!*x₃*…*x_n). So the number of ways to get a three of a kind would be 3!/3! = 6/6 = 1. The number of ways to get a pair would be 3!/(2!*1!) = 6/(2*1) = 3. The number of ways to get three different numbers would be 3!/(1!*1!*1!) = 6/(1*1*1) = 6.

Next we go through the tedious process of adding the number of permutations for each total. For example a total of 6 has the following combinations with the corresponding number of permutations.

The final table will look like this, not unlike the result of the computer function earlier.

So now lets add a column to our list for the number of combinations of each set. Let's also add a total for the three dice.

Now we can divide each total number permutations by the total number 3-dice permutations (216) to get the probability of each total.

Finally, we are ready to evaluate the expected value of each bet. The expected value is the ratio of the amount the player can expect to win to the amount he bets on any given bet. So a fair bet would an expected value of zero. A positive expected value would mean the player has the advantage. A negative expected value would mean the dealer has the advantage.

Let's start with the 4 bet. This wins with a total of 4 and pays 60 to 1. For those who don't know, '60 to 1' means if the player wins he wins 60 times his bet and KEEPS his original wager. Had the odds paid '60 for 1' the player would NOT keep his original bet. Most table games pay on a 'to 1' basis.

The probability of a total of 4 is 3/216 = 0.013889. Thus the probability of losing is 1-(3/216) = 1-0.013889 = 0.986111.

The expected value of any bet with only two possibilities, winning or losing, is:

(Probability of winning)*(Amount of win) + (Probability of losing)*(Amount of loss).

For the 4 bet the expected value is

0.013889 * 60 - 0.986111*-1 = -0.15278.

So, this tells us that for every dollar the player bets on a total of 4 he can expect to lose 15.278 cents on average. Or, the house edge is 15.278%.

The next table shows the expected value and how it was calculated for all bets of a total of 4 to 17.

Two of a kind

There are combin(6,2)=6!/(4!*2!)=15 ways to choose two numbers out of six. Each of these combinations is listed on the table and the player bet on as many as he wishes. If both numbers appear on the roll of the three dice then the player wins and is paid 15 to 1.

Let's assume the player picks a 1 and 2 as his two numbers. What is the probability that both a 1 and 2 occur in the roll of 3 dice? One way to do this would be to note all the possible winning permutations:

Thus there are a total of 30 winning permutations.

There are 6³=216 total permutations, so the probability of winning is 30/216 = 1/36 = 0.1388889

The two of a kind bet pays 5 to 1. So the expected value is 0.1388889*5 + (1-0.1388889)*-1 = -0.16667. In other words the house edge is 16.67%.

Double

There are six double bets available, one for each number from 1 to 6. The player may be on any one or combination of bets. Any given bet wins if at least two of the three dice land on that number.

Let's assume the player bets on the 1.

One way to solve it would be to note all the winning permutations:

Thus there are a total of 16 winning permutations.

There are 6³=216 total permutations, so the probability of winning is 16/216 = 0.0740741.

The double bet pays 10 to 1. So the expected value is 0.0740741*10 + (1-0.0740741)*-1 = -0.18518. In other words the house edge is 18.52% (ouch!).

Triple

Player may bet on any specific number (for example a 1). Player wins if all 3 dice land on that number.

There is obviously only one way to win this bet, so the probability of winning is 1/216 = 0.0046296. The bet pays 180 to 1 so the expected value is 0.0046296*180 + (1-0.0046296)*-1 = -0.16204. So the house edge is 16.204%.

Any Triple

The Any Triple bet pays if any three of a kind is thrown. There are obviously six winning combinations (1,1,1; 2,2,2; 3,3,3; etc.). So the probability of winning is 6/216 = 0.027778. The bet pays 30 to 1 so the expected value is 0.027778*30 + (1-0.027778)*-1 = -0.13889. So the house edge is 13.89%.

Low

The low bet wins if the total of the three dice is 3 to 10, without being a three of a kind. The probability of any total 10 or less is exactly 50%. The average number on any one die is (1+2+3+4+5+6)/6 = 21/6 = 3.5. So the average of three dice is 3*3.5 = 10.5. It stands to reason that the probability of getting under or over 10.5 is 50%.

See Full List On Gambledex.com

However the bet loses on a three of a kind. There are 3 three of a kinds that would turn a winner into a loser: 1,1,1; 2,2,2; and 3,3,3. So the probability of having a total of 10 or less as a three of a kind is 3/216 = 0.0188889. So the overall probability of winning is 0.5 – 0.188889 = 0.4861111. The bet pays 1 to 1 so the expected value is 0.4861111*1 + (1-0.4861111)*-1 = -0.02778. Thus the house edge is 2.78%.

High

The high is just the opposite of the low bet, so it stands to reason the house edge would also be 2.78%.

Individual Number

Player may bet on any specific number from 1 to 6. If chosen number appears 1 time bet pays 1 to 1, if it appears 2 times bet pays 2 to 1, and if it appears 3 times it pays 3 to 1. Probability of 1 match is 34.72%, 2 matches is 6.94%, 3 matches is 0.46%.

Let's assume the player picks the number one.

There is only one way to get three ones: 1,1,1. So the probability of three ones is 1/6³ = 1/216.

Following are the ways to get two 1's and the number of permutations of each.

So the probability of two ones is 15/6³ = 15/216.

Following are the ways to get one 1 and the number of permutations of each.

So the probability of two ones is 75/6³ = 75/216.

Sic Bo Rules And Strategies - Lets Talk Winning

Another way to arrive at the probability of one 1 would be find the probability that the first die is a one and the second and third are not:

Pr(one)*Pr(not one)*Pr(not one) = (1/6)*(5/6)*(5/6) = 25/216.

However the one could appear in the first, second, or third position, so multiply by 3: 3*(25/216) = 75/216.

The probability of rolling zero ones is Pr(not one)*Pr(not one)*Pr(not one) = (5/6)*(5/6)*(5/6) = (5/6)³ = 125/216.

The following return table shows the possible outcomes, and the number of combinations, probability, and return of each. The return is the product of the probability and the win or loss to the player.

So the total expected return is -0.0787, or the house edge is 7.87%.

Sic Bo section at the Wizard of Odds.
How to calcualte the 3-dice permutation in Visual Basic.

Rules and Strategies for
Sic Bo

We are quite used to the game of Craps, that uses two dice. It's challenging enough to find winning strategies with two dice, considering all dice combinations. How about an interesting game that uses three dice? The combinations would be much more intriguing, wouldn't they?

I'm referring to the game called 'Sic Bo', that uses three dice on a layout that is quite different than the Craps layout. Sic Bo has been recently popular in Casino of Montreal. Sic Bo is an ancient Chinese dice game still played in many southeast Asian countries, where it's known as big and small. Sic Bo is both exciting and easy to play, and offers players a wide variety of options. Payouts range from even money up to 150 to 1.

The betting options available at Sic Bo are formed by the various combinations obtained with three dice. These wagers and their payouts are reproduced on the gaming table. Players may wager on as many combinations as desired per game. The dice are shaken by dealer, by means of a vibrating platform under a round shape glass cover. After all bets have been made, the dealer activates the dice shaker. The outcome of each of the three dice appears on the display. At the same time, the spaces corresponding to the winning combinations light up on the table. The dealer then removes all losing bets from the table, such as in roulette, and proceeds to pay all winners.

There are 8 different ways you can bet.

1) You can bet on one number, which must appear on all three dice. This is called a Three of a Kind. Obviously, you have the least chances of hitting a winning bet, as there are 216 (6 X 6 X 6) dice combinations and only one of them can give you a 1,1,1 or 2,2,2 or 3,3,3 or 4,4,4 or 5,5,5 or 6,6,6. If you do win however, it pays 150 to 1. Considering your winning chances to be 1 out of 216, this gives the casino a huge advantage.

2) You can bet on one number, which must appear on two of the three dice. This is called a Two of a Kind, such as a 1,1 or 2,2 or 3,3 or 4,4 or 5,5, or 6,6. This pays 8 to 1, although your chances of winning is 5.82%, as there are 12 ways of making such a combination.

3) You can bet that the same number from 1 to 6 will appear on all three dice, such as either a 1,1,1 or 2,2,2 or 3,3,3 or 4,4,4 or 5,5,5 or 6,6,6. This is called Any Three of a Kind and it pays 24 to 1. You have 6 times more chances to win relative to the Three of a Kind. The probability is still 6 out of 216 or about 2.78%.

4) There is an area called Small, that pays even money, where you bet that the sum of the three dice will be equal to 4, 5, 6, 7, 8, 9, or 10 excluding a Three of a Kind. That's why the 3 (3 ones) is not a winning bet, neither are the hardways 6 and 9, which provides the casino edge.

5) Similarly, there is an area called Big, that also pays even money, where you bet that the sum of the three dice will be equal to 11, 12, 13, 14, 15, 16, or 17 excluding a Three of a Kind. That's why the 18 (3 sixes) is not a winning bet, neither are the hardways 12 and 15, which again provides the casino edge.

6) On the Sic Bo layout, there is a wide area with the numbers 4 to 17 written on them. Those numbers correspond to the sum of the three dice. So, you bet on a number from 4 to 17, which are the sum of all 3 dice and the payout table is as follows:

Sic Bo Dice

• If the sum is 4, winning bets are paid 50 to 1;

• If the sum is 5, winning bets are paid 30 to 1;

• If the sum is 6, winning bets are paid 18 to 1;

• If the sum is 7, winning bets are paid 12 to 1;

• If the sum is 8, winning bets are paid 8 to 1;

• If the sum is 9, winning bets are paid 6 to 1;

• If the sum is 10, winning bets are paid 6 to 1;

• If the sum is 11, winning bets are paid 6 to 1;

• If the sum is 12, winning bets are paid 6 to 1;

• If the sum is 13, winning bets are paid 8 to 1;

• If the sum is 14, winning bets are paid 12 to 1;

• If the sum is 15, winning bets are paid 18 to 1;

• If the sum is 16, winning bets are paid 30 to 1;

• If the sum is 17, winning bets are paid 50 to 1;

You can see the symmetrical pattern of payouts, depending on the dice combinations and their probability of appearance, always with an edge on the casino side, of course.

7) You can bet on two different numbers, which must appear on at least two of the three dice. This bet is called Duo, and it pays 5 to 1. The dice combinations you can bet on are: 1,2 or 1,3 or 1,4 or 1,5 or 1,6 or 2,3 or 2,4 or 2,5 or 2,6 or 3,4 or 3,5 or 3,6 or 4,5 or 4,6 or 5,6, as long as the two numbers are not the same.

8) And the last type of bet is called a simple One of a Kind, where you bet on a single number that must appear on one, two or all three dice. This is shown in the layout as the dice face 1, or 2, or 3, or 4, or 5, or 6.

The payout table of this bet depends on the following:

Cached

• If the number you chose appears on one of the three dice, you are paid even;

• If the number you chose appears on two of the three dice, you are paid 2 to 1;

• If the number you chose appears on three of the three dice, you are paid 3 to 1.

The game is called Sic Bo, meaning Small Big, probably because of the type of bets that pay even - types 4 and 5 above, which could be attractive to bet using our even money bet strategies (Superior Roulette, Reward, etc.). What we need to determine is the percentage of the casino edge, in order to compare this type of bet to Baccarat or Roulette.

Taking the Small bet, we can see that half of all dice combinations will give us a 3 or 4 or 5 or 6 or 7 or 8 or 9 or 10. If we exclude the Three of a Kind, we are excluding the 1,1,1, the 2,2,2 and the 3,3,3. Therefore, we are excluding 3 possibilities out of 108 (216/2). In other words our chances of winning is 105 out of 216 or 48.61%.

Comparing this to roulette, our chances of winning on even bets are 18 out of 37 or 48.64% on a single zero wheel and 18 out of 38 or 47.37% on a double zero wheel. So playing Sic Bo on even money bets such as Small Big is comparable to single zero roulette, the Three of a Kind decision acting as a zero.

So we can easily use any even bet strategy that we have developed for Roulette, that performs even better for single zero wheels.